Domínio e contradomínio de uma função (com exemplos)

Os conceitos de domínio e contradição de uma função Eles são comumente ensinados nos cursos de cálculo ministrados no início das carreiras da universidade.

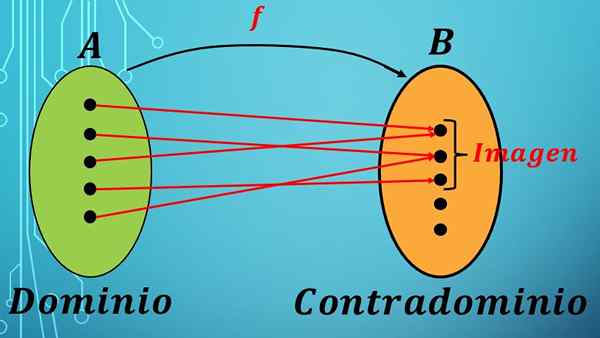
Antes de definir o domínio e contradição, você deve saber o que é uma função. Uma função f é uma lei de correspondência (regra) entre os elementos de dois conjuntos.

O todo do qual os elementos são escolhidos é chamado de domínio da função, e o conjunto para o qual esses elementos são enviados através de F é chamado de contradominium.

Na matemática.

A expressão anterior diz que os elementos do conjunto A são enviados para o conjunto B seguindo a Lei de Correspondência F.

Uma função atribui cada elemento do conjunto a um único elemento do conjunto B.

Domínio e contradição

Dada uma função real de uma variável real f (x), o domínio da função deve ser todos esses números reais de modo que, quando avaliados em f, o resultado é um número real.

Geralmente, a contradição de uma função é o conjunto de N Numbers reais. A contradição também é chamada de chegada ou conjunto de codomínio da função f.

A contradição de uma função é sempre r?

Não. Desde que a função não seja estudada em detalhes, o conjunto de números de N reais geralmente é tomado como contradição.

Mas uma vez que a função é estudada, um conjunto mais apropriado pode ser tomado como contradomínio, que será um subconjunto de r.

O conjunto apropriado mencionado no parágrafo anterior coincide com a imagem da função.

A definição da imagem ou intervalo de uma função f refere -se a todos os valores que vêm da avaliação de um elemento do domínio em f.

Exemplos de domínio e contradição

Nos exemplos a seguir, como calcular o domínio de uma função e sua imagem é ilustrada.

Exemplo 1

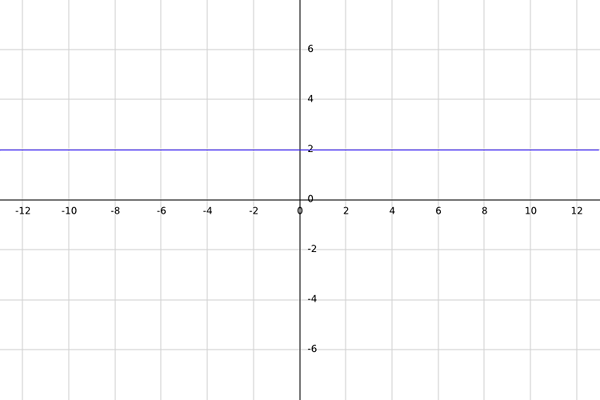
Seja f uma função real definida por f (x) = 2.

O M -Domain de F é todos números reais de modo que, ao avaliá -los em f, o resultado é um número real. A contradição por um momento é igual a r.

Como a função dada é constante (sempre igual a 2), é que não importa que número real seja escolhido, pois ao avaliá -lo no resultado sempre será igual a 2, o que é um número real.

Portanto, o domínio da função dada é todos números reais; isto é, a = r.

Agora que já se sabe que o resultado da função é sempre igual a 2, a imagem da função é apenas o número 2; portanto, a contradição da função pode ser redefinida como b = img (f) = 2.

Portanto, f: r → 2.

Exemplo 2

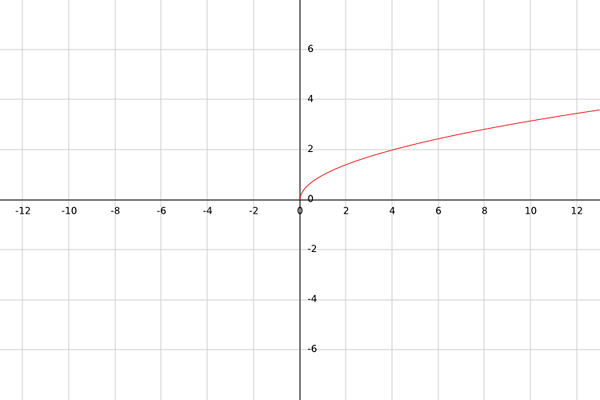
Seja g uma função real definida por g (x) = √x.

Enquanto a imagem de g não for conhecida, o contradomínio de g é b = r.

Com essa função, deve -se levar em consideração que as raízes quadradas são definidas apenas para números não negativos; isto é, para números maiores ou iguais que zero. Por exemplo, √-1 não é um número real.

Portanto, o domínio da função G deve ser todos os números maiores ou iguais que zero; isto é, x ≥ 0.

Portanto, a = [0,+∞).

Para calcular o intervalo, deve -se notar que qualquer resultado de g (x), porque é uma raiz quadrada, sempre será maior ou igual a. Isto é, b = [0,+∞).

Em conclusão, g: [0,+∞) → [0,+∞).

Exemplo 3

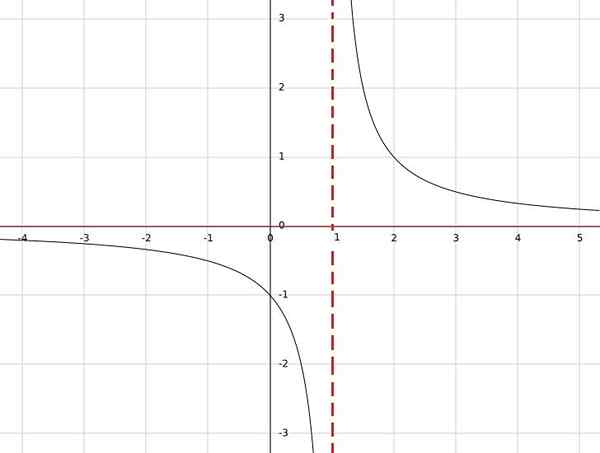
Se você tiver a função H (x) = 1/(x-1), esta função não é definida para x = 1, pois no denominador seria obtido zero e a divisão por zero não é definida.

Por outro lado, para qualquer outro valor real, o resultado será um número real. Portanto, o domínio são todos reais, exceto um; isto é, a = r \ 1.

Do mesmo modo, pode -se observar que o único valor que não pode ser obtido como resultado é 0, pois uma fração é igual a zero, o numerador deve ser zero.

Portanto, a imagem da função é o conjunto de todos os reais, exceto zero, então é considerado contradominium b = r 0.

Em conclusão, h: r \ 1 → r \ 0.

Observações

Domínio e imagem não precisam ser o mesmo conjunto, como demonstrado nos Exemplos 1 e 3.

Quando uma função é gráfica no plano cartesiano, o domínio é representado pelo eixo x e o contradomínio ou a faixa é representada pelo eixo y.