Fórmula de expansão de superfície, coeficientes e exemplos

O dilatação superficial É a expansão que ocorre quando um objeto experimenta variações de sua superfície devido à variação da temperatura. É devido às características do material ou de sua forma geométrica. A dilatação predomina em duas dimensões na mesma proporção.

Por exemplo, em uma folha, quando há uma variação de temperatura, é a superfície da mesma que sofre a maior mudança devido à dilatação térmica.

A superfície de uma placa de metal que geralmente é vista nas ruas. Fonte: Pixabay.

A folha de metal da figura anterior aumenta sua ampla e seu comprimento apreciável quando é aquecida por radiação solar. Pelo contrário, ambos diminuem significativamente quando resfriados devido a uma diminuição na temperatura ambiente.

É por esse motivo que, quando os azulejos são instalados em um andar, algumas bordas com outras não devem ser atingidas, mas deve haver um espaço de separação chamado placa de dilatação.

Além disso, esse espaço é preenchido com uma mistura especial que tem um certo grau de flexibilidade, impedindo que os azulejos rachem devido a fortes pressões que a dilatação térmica pode produzir.

[TOC]

O que é dilatação superficial?

Em um material sólido, os átomos mantêm suas posições relativas mais ou menos fixas em torno de um ponto de equilíbrio. No entanto, devido à agitação térmica, eles estão sempre oscilando em torno disso.

Ao aumentar a temperatura, a oscilação térmica também aumenta, fazendo com que as posições de oscilação média mudem. Isso ocorre porque o potencial de link não é exatamente parabólico e tem assimetria em torno do mínimo.

Abaixo está uma figura que descreve a energia de ligação química, dependendo da distância interatômica. A energia total de oscilação em duas temperaturas também é mostrada e como o centro de oscilação se move.

Pode servir a você: Pascal Tonel: como funciona e experimentos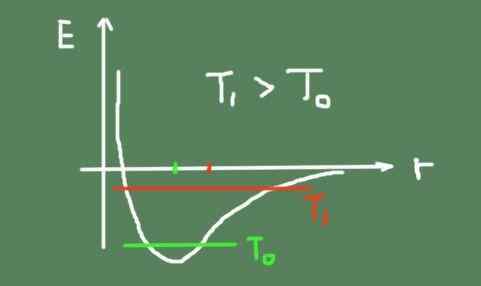Gráfico de energia de ligação versus distância interatômica. Fonte: Self feito.

Dilatação superficial e seu coeficiente

Para medir a dilatação superficial, começamos a partir de uma área inicial A e uma temperatura inicial t, do objeto do qual a dilatação deve ser medida.

Suponha que esse objeto seja uma lâmina da área A, e a espessura é muito menor que a raiz quadrada da área a. A folha é submetida a uma variação de temperatura Δt, de modo que a temperatura final do mesmo assim que o balanço térmico com a fonte de calor será estabelecido será t '= t+ Δt.

Durante esse processo térmico, a área de superfície também terá alterado para um novo valor em '= a + ΔA. Assim, o coeficiente de dilatação da superfície σ é definido como a razão entre a variação relativa da área por unidade de variação de temperatura.

A fórmula a seguir define o coeficiente de dilatação superficial σ:

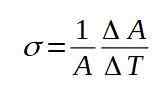
O coeficiente de dilatação superficial σ é praticamente constante para uma ampla gama de valores de temperatura.

Devido à definição de σ, suas dimensões são temperatura inversa. Como unidade, geralmente é usado ° C^-1.

Coeficiente de dilatação de superfície para vários materiais

Em seguida, daremos uma lista do coeficiente de dilatação superficial para alguns materiais e elementos. O coeficiente é calculado na pressão atmosférica normal com base em uma temperatura ambiente de 25 ° C, e seu valor é considerado constante em uma faixa de ΔT de -10 ° C a 100 ° C.

A unidade do coeficiente de dilatação superficial será (° C)^-1

- Aço: σ = 24 ∙ 10^-6 (° C)^-1

- Alumínio: σ = 46 ∙ 10^-6 (° C)^-1

Pode servir a você: Magnetização: Orbital e Moment Magnético, Exemplos

- Ouro: σ = 28 ∙ 10^-6 (° C)^-1

- Cobre: ​​σ = 34 ∙ 10^-6 (° C)^-1

- Brass: σ = 36 ∙ 10^-6 (° C)^-1

- Ferro: σ = 24 ∙ 10^-6 (° C)^-1

- Vidro: σ = (14 a 18) ∙ 10^-6 (° C)^-1

- Quartzo: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamante: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Lead: σ = 60 ∙ 10^-6 (° C)^-1

- Madeira de carvalho: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Fibra de carbono: σ = -1,6 ∙ 10^-6 (° C)^-1

- Concreto: σ = (16 a 24) ∙ 10^-6 (° C)^-1

A maioria dos materiais se estende com um aumento de temperatura. No entanto, alguns materiais como a fibra de carbono atendem ao aumento da temperatura.

Exemplos resolvidos de dilatação superficial

Exemplo 1

Uma placa de aço tem dimensões de 3m x 5m. De manhã e à sombra, sua temperatura é de 14 ° C, mas ao meio -dia o sol aquece até 52 ° C. Encontre a área final da placa.

Solução

Começamos a partir da definição de coeficiente de dilatação superficial:

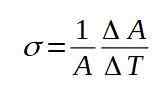
A partir daqui, limpamos a variação na área:

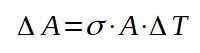
Em seguida, passamos a substituir os respectivos valores para encontrar o aumento da área com o aumento da temperatura.

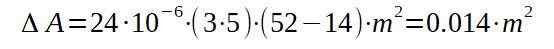
Isto é, a área final será de 15.014 metros quadrados.

Exemplo 2

Mostre que o coeficiente de dilatação superficial é aproximadamente o dobro do coeficiente de dilatação linear.

Solução

Suponha que começamos a partir de uma placa retangular de dimensões de largura lx e longa, então sua área inicial será a = lx ∙ ly

Pode atendê -lo: escalas termométricas

Quando a placa sofre um aumento de temperatura Δt, suas dimensões também aumentam sendo sua nova largura LX 'e seu novo por muito tempo, de modo que sua nova área será a' = lx '' ly '

A variação sofrida pela área da placa devido à mudança de temperatura será então

ΔA = lx '∙ ly' - lx ∙ ly

onde lx '= lx (1 + α Δt) e ly' = ly (1 + α Δt)

Ou seja, que a mudança de área, dependendo do coeficiente de dilatação linear e da mudança de temperatura: será:

ΔA = lx (1 + α Δt) ∙ ly (1 + α Δt) - lx ∙ ly

Isso pode ser reescrito como:

ΔA = lx ∙ ly ∙ (1 + α Δt) ² - lx ∙ ly

Desenvolvendo o quadrado e multiplicando, temos o seguinte:

EU

Como α é da ordem de 10^-6, Ao levantá -lo quadrado, é a ordem de 10^-12. Assim, o termo quadrático na expressão anterior é desprezível.

Em seguida, o aumento da área pode ser abordado por:

ΔA ≈ 2α Δt lx ∙ ly

Mas o aumento da área, dependendo do coeficiente de dilatação superficial é:

ΔA = γ ΔT A

De onde é deduzido uma expressão que relaciona o coeficiente de dilatação linear ao coeficiente de dilatação superficial.

γ ≈ 2 ∙ α

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mac Graw Hill. 422-527
2. Giancoli, d. 2006. Física: Princípios com aplicações. 6º. Edição. Prentice Hall. 238-249.