Derivados algébricos

O que são derivados algébricos?

As derivados algébricos Eles consistem no estudo da derivada no caso particular de funções algébricas. A origem da noção de derivada remonta à Grécia antiga. O desenvolvimento dessa noção foi motivado pela necessidade de resolver dois problemas importantes, um em física e outro em matemática.

Na física, o derivado resolve o problema de determinar a velocidade instantânea de um objeto em movimento. Em matemática, permite encontrar a linha tangente em uma curva em um determinado ponto.

Embora existam realmente muito mais problemas que são resolvidos usando o derivado, bem como suas generalizações, resultados que vieram mais tarde para a introdução de seu conceito.

Os pioneiros do cálculo diferencial são Newton e Leibniz. Antes de dar a definição formal, desenvolveremos a idéia por trás, do ponto de vista matemático e físico.

O derivado como pendente da linha tangente para uma curva

Suponha que o gráfico de uma função y = f (x) seja um gráfico contínuo (sem picos, vértices ou separações) e a = (a, f (a)) um ponto fixo sobre ele. Queremos encontrar a equação de linha tangente para a função f no ponto a.

Vamos tomar outro ponto p = (x, f (x)) do gráfico, próximo ao ponto A, e rastrear a linha de secagem que passa por A e P. Uma linha de secagem é uma linha que corta o gráfico de uma curva em um ou mais pontos.

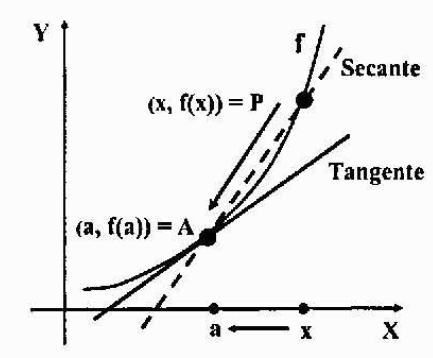
Para obter a linha tangente que queremos, é necessário apenas calcular a inclinação porque já temos um ponto da linha: o ponto a.

Se movermos o ponto P pelo gráfico e abordarmos cada vez mais para o ponto A, a linha seca mencionada anteriormente se aproximará da linha tangente que você deseja encontrar. Tomando o limite quando "p tende a um", ambas as linhas coincidem, portanto suas encostas também.

A inclinação da linha secante é dada por

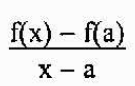
Dizer que P está próximo de A, é equivalente a dizer que "x" se aproxima "a". Assim, a inclinação da linha tangente para o gráfico de f no ponto A será igual a:

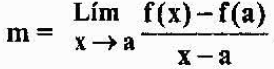
A expressão anterior é denotada por f '(a) e é definida como a derivada de uma função f no ponto "a". Vemos que analiticamente, o derivado de uma função em um ponto é um limite, mas geometricamente, é a inclinação da linha tangente ao gráfico da função no ponto.

Pode servir a você: variável aleatória: conceito, tipos, exemplos

Agora veremos essa noção do ponto de vista da física. Atingiremos a mesma expressão do limite anterior, embora por um caminho diferente, obtendo assim a unanimidade da definição.

O derivado como velocidade instantânea de um objeto em movimento

Vejamos um breve exemplo do que significa velocidade instantânea. Quando é dito, por exemplo, que um carro para chegar a um destino o fez com uma velocidade de 100 km por hora, o que significa é que em uma hora ele viajou 100 km.

Isso não significa necessariamente que, durante toda a hora, o carro estava sempre 100 km, o vecímetro do carro poderia em alguns momentos marcar menos ou mais. Se ele tivesse a necessidade de ficar com um semáforo, a velocidade naquele momento era de 0 km. No entanto, depois de uma hora, a rota era de 100 km.

Isso é conhecido como velocidade média e é dado pelo quociente da distância percorrida entre o tempo decorrido, como acabamos de ver. A velocidade instantânea, enquanto isso, é a que marca a agulha de velocímetro de um carro em um certo instante (tempo).

Vamos ver isso agora mais geral. Suponha que um objeto se mova ao longo de uma linha e que esse deslocamento seja representado por meio da Equação S = F (T), onde a variável t mede o tempo e a variável S o deslocamento, levando em consideração seu começo no momento t = 0, quando também é zero, ou seja, f (0) = 0.

Esta função f (t) é conhecida como função de posição.

Uma expressão para a velocidade instantânea do objeto é procurada em um instante fixo. Nesta velocidade, nós o indicaremos por v (a).

Seja a qualquer momento próximo ao instante "A". No intervalo de tempo entre "a" e "t", a mudança de posição é dada por f (t) -f (a).

A velocidade média neste intervalo de tempo é:

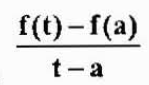
Que é uma aproximação da velocidade instantânea v (a). Esta abordagem será melhor à medida que T se aproxima de "A". Portanto,

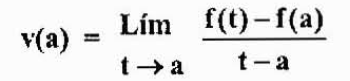
Vamos perceber que essa expressão é igual à obtida no caso anterior, mas de uma perspectiva diferente. É isso que é conhecido como o derivado de uma função f em um ponto "a" e é denotado por f '(a), como afirmado acima.

Pode atendê -lo: leis de expoentes

Observe que fazer a mudança h

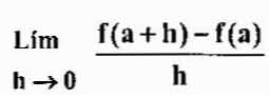
Ambas as expressões são equivalentes, mas às vezes devem ser usadas mais para uma do que a outra, dependendo do caso.

Então é definido de maneira mais geral que derivou de uma função f em qualquer ponto "x" pertencente ao seu domínio como

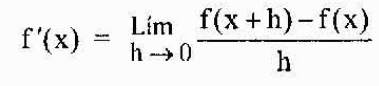
A notação mais usual para representar a derivada de uma função y = f (x) é a que acabamos de ver (f 'o y'). No entanto, outra notação amplamente utilizada é a notação de Leibniz representada como qualquer uma das seguintes expressões:

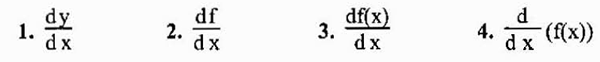
Em vista do fato de que o derivado é em essência um limite, pode ou não existir, pois os limites nem sempre existem. Caso exista, diz -se que a função em questão é diferenciável no ponto determinado.

Função algébrica

Uma função algébrica é uma combinação de polinômios através de somas, subtrações, produtos, quocientes, poderes e radicais.

Um polinômio é uma expressão de forma

P_n= a_nxⁿ+ para_N-1x^N-1+ para_N-2x^N-2+… + A₂x²+ para₁x+a₀

Onde n é um número natural e todo o_Yo, Com i = 0,1,…, n são números racionais e_n≠ 0. Nesse caso, diz -se que o grau deste polinômio é n.

A seguir, são apresentados exemplos de funções algébricas:

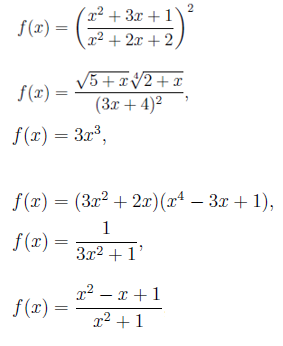
Aqui as funções exponenciais, logarítmicas e trigonométricas não estão incluídas. As regras de derivação que veremos abaixo são válidas para funções em geral, mas vamos restringir e aplicá -las no caso de funções algébricas.

Regras de derrying

Derivado de uma constante

Afirma que o derivado de uma constante é zero. Isto é, se f (x) = c, então f '(x) = 0. Por exemplo, o derivado da função constante 2 é igual a 0.

Derivado de um poder

Se f (x) = xⁿ, então f '(x) = nx^N-1. Por exemplo, x derivado³ É 3x². Como conseqüência disso, obtém -se que o derivado da função de identidade f (x) = x é f '(x) = 1x^1-1= x⁰= 1.

Outro exemplo é o seguinte: deixe f (x) = 1/x², então f (x) = x^-2 e f '(x) = -2x^-2-1= -2x^-3.

Esta propriedade também é raízes válidas, pois as raízes são poderes racionais e o acima também pode ser aplicado nesse caso. Por exemplo, o derivado de uma raiz quadrada é dada por

Pode atendê -lo: estimativa por intervalos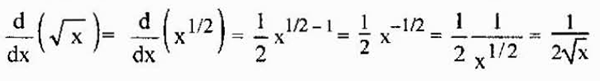

Derivado de uma soma e uma subtração

Se f e g são funções diferenciáveis ​​em x, a soma f+g também é e é cumprido que (f+g) '(x) = f' (x)+g '(x) (x) (x).

Da mesma forma, você precisa (f -g) '(x) = f' (x) -g '(x). Em outras palavras, o derivado de uma soma (subtração) é a soma (ou subtração) dos derivados.

Exemplo

Se h (x) = x²+X-1, então

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produto derivado de um produto

Se F e G são funções diferenciáveis ​​em x, o produto FG também é diferenciável em x e é cumprido que

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Como conseqüência, ele tem se c é uma constante e f é uma função diferenciável em x, então CF também é diferenciável em x Y (cf) '(x) = cf' (x).

Exemplo

Se f (x) = 3x (x²+1) então

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Derivado de um quociente

Se f e g são diferenciáveis ​​em x e g (x) ≠ 0, então f/g também é diferenciável em x, e é cumprido que

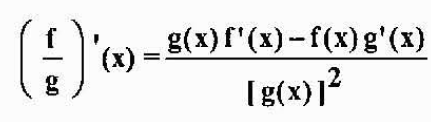
Exemplo: Se h (x) = x³/(x²-5x), então

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Regra da cadeia

Esta regra permite derivar a composição das funções. Estabelece o seguinte: se y = f (u) for diferenciável em u, e u = g (x) for diferenciável em x, então a função composta f (g (x)) é diferenciável em x, e é cumprido que [f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f g (x)]] '= f' (g (x)) g '(x).

Ou seja, o derivado de uma função composta é o produto da derivada da função externa (derivada externa) pela função interna derivada (derivada interna).

Exemplo

Se f (x) = (x⁴-2x)³, então

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Também existem resultados para calcular o derivado conversador de uma função, bem como a generalização para derivados de ordem superior. As aplicações são extensas. Entre eles, seus lucros em otimização e funções mínimas são destacadas.

Referências

1. Alarcon, s., González, m., & Quintana, H. (2008). Cálculo diferencial. ITM.
2. Cabrera, v. M. (1997). 4000 cálculo. Editorial Progreso.
3. Castaño, h. F. (2005). Matemática antes do cálculo. Universidade de Medellin.
4. Eduardo, n. PARA. (2003). Introdução ao cálculo. Edições de Umbral.
5. Fontes, a. (2016). MATEMÁTICA BÁSICA. Uma introdução ao cálculo. Lulu.com.
6. Purcell, e. J., Rigdon, s. E., & Varberg, D. E. (2007). Cálculo. Pearson Education.
7. Saenz, J. (2005). Cálculo diferencial (Segunda ed.). BarQuisimeto: hipotenusa.
8. Thomas, g. B., & Weir, M. D. (2006). Cálculo: várias variáveis. Pearson Education.