Pagina inicial
Matemática
Decágono regular e irregular, propriedades, exemplos

Matemática

Decágono regular e irregular, propriedades, exemplos

4465
1128
Tim Mann

Ele decágono É uma figura plana com um polígono em forma de 10 lados e 10 vértices ou dicas. Os decagonos podem ser regulares ou irregulares; no primeiro caso, todos os lados e ângulos internos têm a mesma medida, enquanto no segundo os lados e/ou os ângulos são diferentes um do outro.

A Figura 1 mostra exemplos de decagnes de cada tipo e, como podemos ver, o decágono comum é muito simétrico.

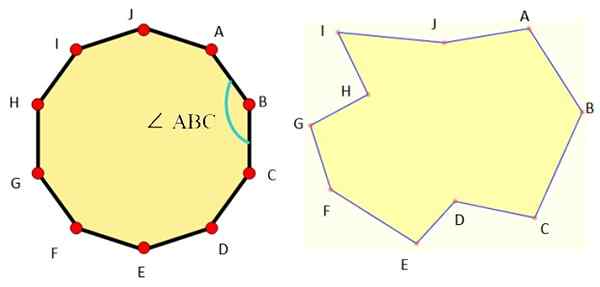figura 1. À esquerda um decágono regular e à direita um decágono irregular. Fonte: Wikimedia Commons/F. Zapata/MathpenRef.

Os elementos básicos de todo o Decágono são:

-Lados, os segmentos de linha que, ao ingressar no decágono.

-Vértices, ou pontos entre cada lado consecutivo.

-Ângulos internos e externos entre lados adjacentes.

-Diagonais, segmentos que unem dois vértices não consecutivos.

Os vértices são chamados por letras maiúsculas, como mostrado na Figura 1, onde foram usadas as primeiras letras do alfabeto, mas qualquer letra pode ser usada.

Os lados são simbolizados com as duas letras dos vértices, entre os quais estão, por exemplo, o lado ab é o entre os vértices a e b. Da mesma maneira que é feito com as diagonais, então temos a AF diagonal, que se junta aos pontos A e F.

Para ângulos, usamos este símbolo: porte semelhante a um L inclinado. Por exemplo, o ângulo porte ABC é aquele cujo vértice é B e cujos lados são os segmentos AB e BC.

[TOC]

Decágono regular

No decágono regular, todos os lados têm a mesma medida, bem como ângulos internos. Portanto, diz -se que é equilátero (lados iguais) e equiângulo (Ângulos iguais). É uma figura muito simétrica

Ângulos internos de um decágono regular

Para encontrar a medida dos ângulos internos de um polígono regular, incluindo o decágono regular, a seguinte fórmula é usada:

$I=\frac(n-2)\times 180^^on$

Onde:

-Eu sou a medida do ângulo em graus.

-n é o número de lados do polígono. No caso do decágono n = 10.

Pode servir você: heptagon

Substituindo n = 10 Na fórmula anterior, obtemos o seguinte:

$I=\frac(10-2)\times 180^^o10=144^^o$

Agora, diz -se que um polígono é convexo Se suas medidas angulares forem inferiores a 180º, caso contrário, o polígono será côncavo. Como qualquer ângulo interno do decágono regular mede 144º e é menor que 180º, então é um polígono convexo.

Soma de ângulos internos

A soma das medidas dos ângulos internos de qualquer polígono é, em graus:

S = (n-2) x 180º; n é sempre maior que 2

Nesta fórmula, temos que:

-S é a soma das medidas dos ângulos internos.

-n é o número de lados. Para o decágono n = 10

Aplicando a fórmula para n = 10 resultados:

S = (10 - 2) x 180º = 1440º

Ângulos externos

Um ângulo externo é formado entre um lado e a extensão do lado adjacente, vamos ver:

Figura 2.- O ângulo externo do decágono regular mede 36º. Fonte. Wikimedia Commons/F. Zapata.

O ângulo porte ABC mais o ângulo externo adiciona 180º, ou seja, eles são Suplementar. Portanto, o ângulo externo é igual a 180º-144º = 36º, como vemos na figura.

Número de diagonais

Como afirmado anteriormente, as diagonais são os segmentos que unem vértices não consecutivos. Quantas diagonais podemos rastrear em um decágono? Quando o número de vértices é pequeno, eles podem ser facilmente contados, mas quando esse número aumenta, você pode perder a conta.

Felizmente, há uma fórmula para saber o número de diagonais que um polígono tem n laterais:

$D=\fracn(n-3)2$

Para o decágono, substituímos n = 10 e obtemos:

D = 10 x (10 - 3) /2 = 35

No decágono regular, todas as diagonais são cortadas em um ponto, que é o centro da figura:

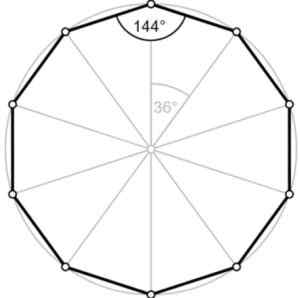Figura 3. Ângulos e diagonais do decágono regular. Fonte: Wikimedia Commons.

Centro

O centro de um polígono é definido como aquele ponto equidistante de qualquer vértice. Na figura anterior, o centro coincide com o ponto de interseção de todas as diagonais.

Perímetro

Se o decágono regular tiver o lado a, seu perímetro P é a soma de todos os lados:

Pode atendê -lo: 90 divisores: o que são e explicação

P = 10.para

Área

Conhecendo o comprimento para Por lado, a área regular do decágono é calculada por:

$A=\left (\frac52 \right )cot\left ( \frac\pi 10 \right )a^2$

Uma fórmula aproximada para a área é:

$A=\frac10a^24 \times tg\left ( \frac\pi 10 \right )\simeq 7.694a^2$

E uma terceira opção para encontrar a área é pela duração do apothem L_PARA. Este é o segmento que se junta ao ponto médio de um lado com o centro do polígono.

Nesse caso, a área pode ser calculada usando a fórmula:

$A=\fracP.L__A2=\frac10a\times L_A2$

Decágono irregular

O decágono irregular não é equilateral ou equiangle e, em geral.

Eles também podem ser convexos ou côncavos, se houver ângulos internos maiores que 180º.

O decágono irregular da Figura 1 é côncavo, pois alguns de seus ângulos internos são maiores que 180º. É evidente que existem muitas combinações de ângulos e lados que dão origem a um decágono irregular.

De qualquer forma, é cumprido que:

-Os ângulos internos de um decágono irregular também adicionam 1440º.

-Ele também tem 35 diagonais.

Área de um decágono irregular por determinantes de Gauss

Em geral, não existe uma fórmula única para encontrar a área de um polígono irregular, pois os lados e os ângulos são diferentes. No entanto, você pode encontrar o conhecimento das coordenadas dos vértices e calculando o Determinantes de Gauss:

-Vamos ligar (x_n , e_n) para as coordenadas dos vértices, com n variando de 1 a 10.

-Você pode começar de qualquer vértice, para o qual as coordenadas serão atribuídas (x x₁, e₁). Agora você deve substituir os valores de cada coordenada nesta fórmula:

$A=\left |\frac(x_1y_2-x_2y_1)+(x_2y_3-x_3y_2)+(x_3y_4-x_4y_3)+… (x_ny_1-x_1y_n)2 \right |$

Onde os determinantes são precisamente as operações entre parênteses.

-É importante observar que o último determinante envolve o primeiro vértice juntamente com o último. Para o decágono, seria assim:

(x₁₀e₁ - x₁e₁₀)

Pode atendê -lo: interpolação de Lagrange

Importante: As barras são de valor absoluto e significam que o resultado final está sempre com um sinal positivo.

O procedimento pode ser trabalhoso quando a figura tem muitos vértices; no caso do decágono, existem 10 operações, por isso é aconselhável fazer uma tabela ou uma lista.

Exercício resolvido

Calcule a área irregular do decágono mostrado na figura. As coordenadas dos vértices são A, B, C ... J, cujos valores são mostrados à esquerda.

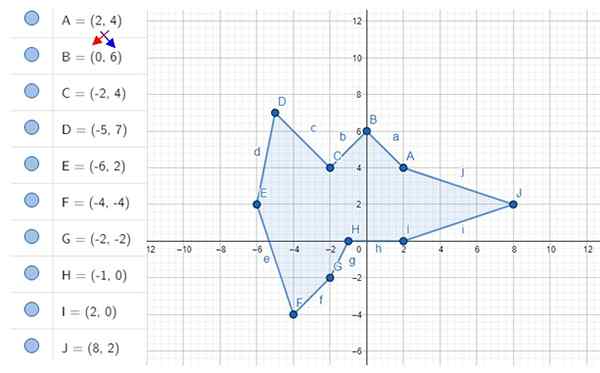Figura 4. Decágono irregular e seus vértices. Fonte: f. Zapata com geogebra.

Solução

-Fazemos cada uma das 10 operações:

2 × 6 - 4 × 0 = 12 - 0 = 12
0 × 4 - 6 × (-2) = 0 + 12 = 12
(-2) × 7- 4 × (-5) = -14 + 20 = 6
(-5) × 2 -7 × (-6) = -10 + 42 = 32
(-6) × (-4) -2 × (-4) = 24 + 8 = 32
(-4) × (-2)-(-4) × (-2) = 8-8 = 0
(-2) × 0-(-2) × (-1) = 0 -2
(-1) × 0 - 0 × (2) = 0 - 0 = 0
2 × 2 - 0 × 8 = 4 - 0 = 4
8 × 4 -2 × 2 = 32 - 4 = 28

-Adicionamos os resultados:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Um resultado positivo é obtido mesmo sem as barras de valor absoluto, mas se for negativo, o mesmo é alterado.

-O resultado anterior é dividido por 2 e essa é a área do polígono:

A = 124/2 = 62

Propriedades de decango

Abaixo está o resumo das propriedades gerais de um decágono, seja regular ou irregular:

-Tem 10 lados e 10 vértices.

-A soma dos ângulos internos é 1440º.

-Existem 35 diagonais.

-O perímetro é a soma de todos os lados.

-Você pode criar triângulos dentro de um segmentos de desenho de polígonos de um vértice para todos os outros. Em um decágono, é possível desenhar 8 triângulos dessa maneira, como mostrado abaixo:

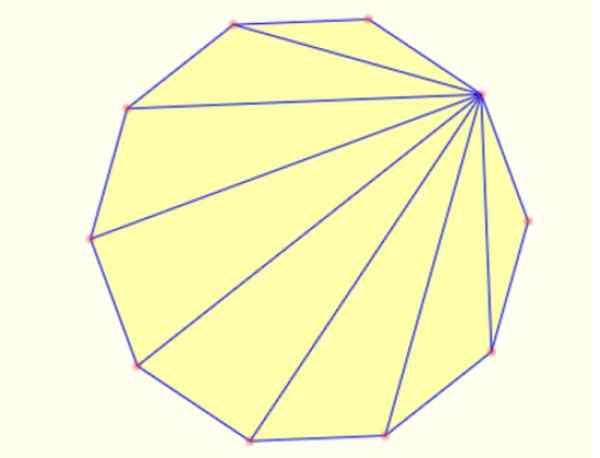Figura 5. Triângulos internos em um decágono regular. Fonte: MathpenRef.

Referências

Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
Decágono.com. Decágono. Recuperado de: Decágono.com
Math Open Reference. Decágono. Recuperado de: MathpenRef.com.
Sangaku Maths. Elementos de um polígono e sua classificação. Recuperado de: sangakoo.com.
Wikipedia. Decágono. Recuperado de: é.Wikipedia.com.