Elementos quadrilaterais, propriedades, classificação, exemplos

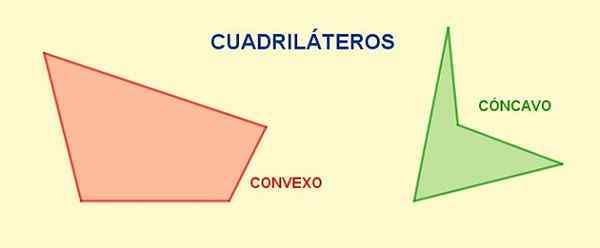
A quadrilátero É um polígono de quatro e quatro vértices. Deles lados opostos Eles são aqueles que não têm vértices comuns, enquanto são lados consecutivos Aqueles que têm um vértice comum.

Em um quadrilateral eles são ângulos adjacentes Aqueles que compartilham um lado, enquanto ângulos opostos Eles não têm lados comuns. Outra característica importante de um quadrilateral é que a soma de seus quatro Ângulos internos É o dobro do ângulo plano, que é 360º ou 2π radianos.

figura 1. Vários quadriláteros. Fonte: f. Zapata.

As diagonais São os segmentos que unem um vértice com seu oposto e em um determinado anel, de cada vértice, você pode desenhar uma única diagonal. O número total de diagonais de um quadrilateral é dois.

Os quadriláteros são números conhecidos pela humanidade desde os tempos antigos. Registros arqueológicos, bem como as construções que sobrevivem hoje, atestam.

Hoje também os quadrilásteros continuam a ter uma presença importante na vida cotidiana de todos. O leitor pode encontrar este formulário na tela em que o texto lê neste momento preciso, nas janelas, nas portas, nas peças automotivas e inúmeros lugares mais.

[TOC]

Classificação de quadriláteros

De acordo com o paralelismo dos lados opostos, os quadriláteros são classificados da seguinte forma:

1. Trapézio, Quando não há paralelismo e o quadrilátero é convexo.
2. Trapézio, Quando há paralelismo entre um único par de lados opostos.
3. Paralelogramo, Quando seus lados opostos são paralelos dois a dois.

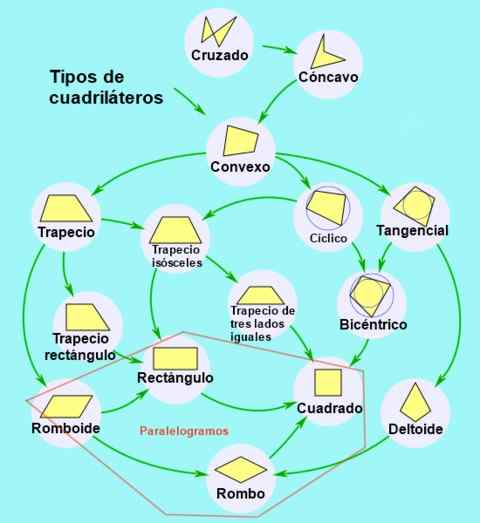Figura 2. Classificação e subclassificação de quadriláteros. Fonte: Wikimedia Commons.

Tipos de paralelogramo

Por sua vez, os paralelogramas podem ser classificados de acordo com seus ângulos e laterais da seguinte forma:

1. Retângulo, É o paralelogramo que tem seus quatro ângulos internos de igual medida. Os ângulos internos de um retângulo formam um ângulo reto (90º).
2. Quadrado, É um retângulo com seus quatro lados de igual medida.
3. Diamante, É o paralelogramo com seus quatro lados, mas seus diferentes ângulos adjacentes.
4. Rombóide, paralelogramo com diferentes ângulos adjacentes.

Trapézio

O trapézio é um quadrilátero convexo com dois lados paralelos.

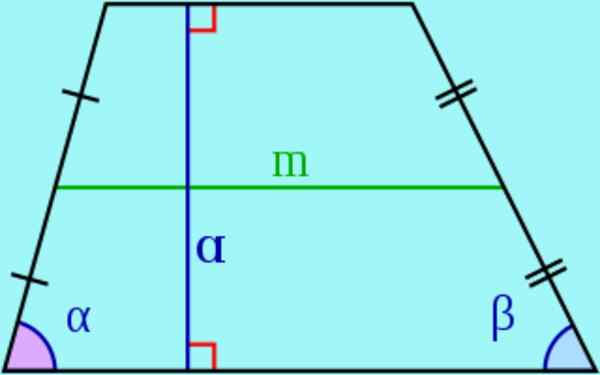Figura 3. Bases, lateral, altura e mediana de um trapézio. Fonte: Wikimedia Commons.

- Em um trapézio, os lados paralelos são chamados bases E os não paraléis são chamados lateral.

- O altura de um trapez. Este segmento também é chamado de altura do trapézio.

- O mediana É o segmento que se junta aos pontos médios dos lados. Pode -se demonstrar que a mediana é paralela às bases do trapézio e seu comprimento é igual aos corpos semi -Bases.

- A área de um trapézio é sua altura multiplicada pelos corpos semi -Bases:

Área de um trapézio = altura * (base 1 + base 2) / 2

Tipos de trapézio

-Trapézio retângulo: É o que tem um lado perpendicular às bases. Este lado também é a altura do trapézio.

-Isósceles de trapézio: Aquele com lados iguais de comprimento. Em um trapézio isósceles, os ângulos adjacentes às bases são iguais.

-Escaleno Trapezio: Aquele que tem seus lados de comprimento diferente. Seus ângulos opostos podem ser agudos e o outro obtuso, mas também pode acontecer que ambos sejam obtusos ou agudos.

Pode atendê -lo: exercícios de fatoração resolvidos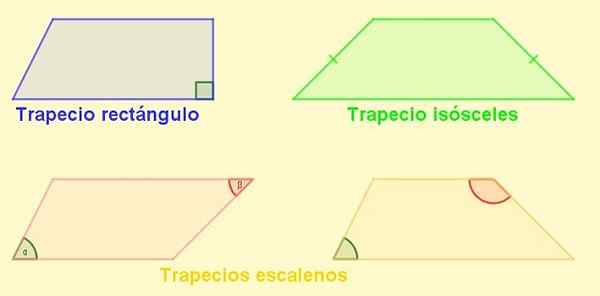 Figura 4. Tipos de trapézio. Fonte: f. Zapata.

Paralelogramo

O paralelogramo é um quadrilateral cujos lados opostos são paralelos dois a dois. Em um paralelogramo, os ângulos opostos são os mesmos e os ângulos adjacentes são suplementares, ou, em outras palavras, os ângulos adjacentes totalizam 180º.

Se um paralelogramo tiver um ângulo reto, todos os outros ângulos também serão e a figura resultante será chamada retângulo. Mas se o retângulo também tiver seus lados adjacentes do mesmo comprimento, todos os seus lados são iguais e a figura resultante é um quadrado.

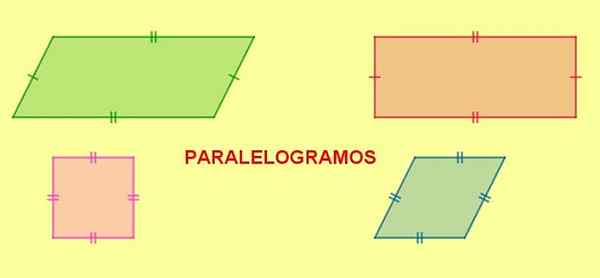Figura 5. Paralelogramas. O retângulo, o quadrado e o rombus são paralelogramas. Fonte: f. Zapata.

Quando um paralelogramo tem dois lados adjacentes do mesmo comprimento, todos os seus lados terão o mesmo comprimento e a figura resultante é um diamante.

A altura de um paralelogramo é um segmento com pontas em seus lados opostos e perpendicularmente.

Uma área de paralelograma

A área de um paralelogramo é o produto da base por sua altura, sendo a base um lado perpendicular à altura (Figura 6).

Área de um paralelogramo = base x altura = a . h

Diagonais de um paralelogramo

O quadrado da diagonal que começa em um vértice é igual à soma dos quadrados dos dois lados adjacentes ao dito vértice a mais o duplo produto daqueles lados pelo cosseno do ângulo daquele vértice:

F² = a² +  d² + 2 A D cos (α)

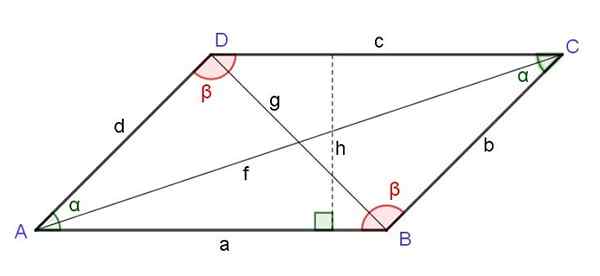Figura 6. Paralelogramo. Ângulos opostos, altura, diagonais. Fonte: f. Zapata.

O quadrado da diagonal oposto ao vértice de um paralelogramo é igual à soma dos quadrados dos dois lados adjacentes ao referido vértice e subtraiu o produto duplo daqueles lados pelo cosseno do ângulo desse vértice:

g² = a² + d² - 2 A D cos (α)

Lei dos Paralelogramas

Em qualquer paralelogramo, a soma dos quadrados de seus lados é igual à soma dos quadrados das diagonais:

para² + b² + c² + d² = f² + g²

Réctangle

O retângulo é um quadrilátero com seus lados opostos paralelos dois a dois e que também tem um ângulo reto. Ou seja, o retângulo é um tipo de paralelograma com um ângulo reto. Por ser paralelogramo, O retângulo tem seus lados opostos de igual comprimento a = c e b = d. 

Mas, como em qualquer paralelogramo, os ângulos adjacentes são suplementares e os ângulos opostos iguais, no retângulo por ter um ângulo reto, ele necessariamente formará ângulos retos nos outros três ângulos. Quer dizer Em um retângulo, todos os ângulos internos medem 90º ou π/2 radianos.

Diagonais de um retângulo

Em um retângulo, as diagonais são iguais, Como será demonstrado abaixo. O raciocínio é o seguinte; Um retângulo é um paralelogramo com todos os seus ângulos retos e é por isso que herda todas as propriedades do paralelogramo, incluindo a fórmula que dá o comprimento das diagonais:

F² = a²+  d² + 2 A D cos (α)

g² = a² + d² - 2 A D cos (α)

com α = 90º

Como Cos (90º) = 0, Então acontece que:

F² = g² = a² +  d²

Quer dizer que f = g, e, portanto, os comprimentos F e g Das duas diagonais do retângulo, elas são iguais e seu comprimento é dado por:

Comprimento diagonal de um retângulo = √ (a² + b²)

Além disso, se em um retângulo de lados adjacentes para e b Um lado é baseado no outro lado será a altura e, consequentemente, a área do retângulo será:

Pode servir a você: Fibonacci Series: Propriedades, Relacionamentos naturais, aplicações

Área de retângulo = a x b.

O perímetro é a soma de todos os lados do retângulo, mas como os opostos são os mesmos, é então necessário para um retângulo de um lados para e b O perímetro é dado pela seguinte fórmula:

Perímetro de retângulo = 2 (a + b)

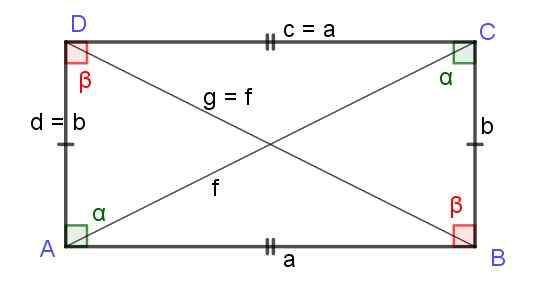Figura 7. Retângulo de lados a e b. As diagonais f e g são iguais. Fonte: f. Zapata.

Quadrado

O quadrado é um retângulo com seus lados adjacentes do mesmo comprimento. Se o quadrado tiver lado para, Então suas diagonais F e g Eles têm o mesmo comprimento, que é F = g = (√2) a.

A área de um quadrado é o lado elevado ao quadrado:

Área de um quadrado = A²

O perímetro de um quadrado é o dobro do lado:

Perímetro de um quadrado = 4 a

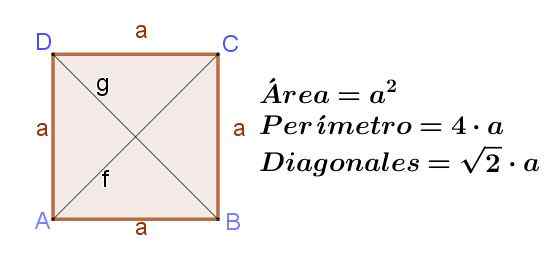Figura 8. Quadrado a lado a, indicando sua área, seu perímetro e o comprimento de suas diagonais. Fonte: f. Zapata ..

Diamante

O RHombus é um paralelogramo com seus lados adjacentes do mesmo comprimento, mas como em um paralelogramo os lados opostos são os mesmos então, Todos os lados de um rombus são iguais.

As diagonais de um rombus são de comprimento diferente, mas são cortadas em ângulos retos.

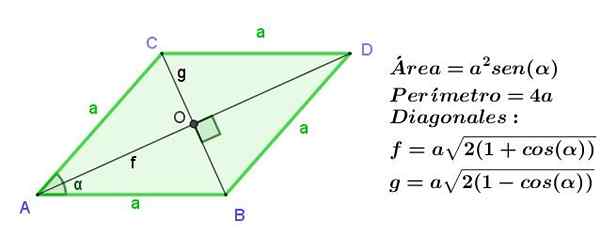Figura 9. RHombus do lado a, indicando sua área, perímetro e o comprimento de suas diagonais. Fonte: f. Zapata.

Exemplos

Exemplo 1

Demonstrar que em um quadrilateral (não cruzado) os ângulos internos totalizam 360º.

Figura 10: É demonstrado como a soma dos ângulos de um quadrilateral adicionar 360º. Fonte: f. Zapata.

ABCD é considerado um ABCD (veja a Figura 10) e o BD diagonal é desenhado. Dois triângulos ABD e BCD são formados. A soma dos ângulos internos do triângulo ABD é:

α + β₁ + δ₁ = 180º

E a soma dos ângulos internos do triângulo BCD é:

 β2 + γ + δ₂ = 180º

Adicionando as duas equações é obtido:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Agrupamento:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Agrupando e renovação, finalmente é demonstrado que:

α + β + Δ + γ = 360º

Exemplo 2

Demonstre que a mediana de um trapézio é paralelo às suas bases e seu comprimento é o semi -sísmico das bases.

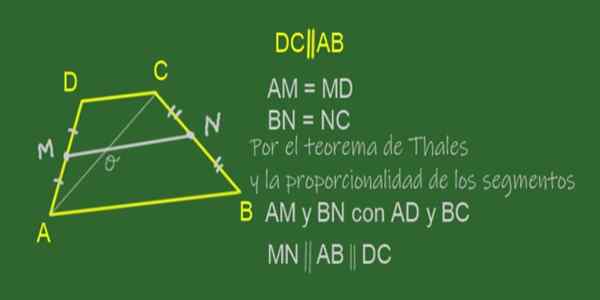Figura 11. MN mediano do trapézio ABCD. Fonte: f. Zapata.

A mediana de um trapézio é o segmento que se junta aos pontos médios de seus lados, ou seja, os lados não paralelos. No trapézio ABCD mostrado na Figura 11, a mediana é MN. 

Por ser um ponto médio de anúncio e n médio de ponto aC, é cumprido que os quocientes AM / AD e BN / BC são iguais.

Ou seja, a AM é proporcional ao BN na mesma proporção que o AD é BC; portanto, as condições para a aplicação do teorema (recíproco) de Thales que afirmam o seguinte:

"Se em três ou mais cortes retos por dois secantes".

No nosso caso, conclui -se que as linhas Mn, AB e CC são paralelas entre si: portanto:

"EUem uma mediana de um trapézio é paralelo às suas bases".

Pode atendê -lo: operações combinadas

Agora o teorema de Thales se aplicará:

"Um conjunto de paralelos cortados por dois ou mais secagem determina segmentos proporcionais".

No nosso caso, anúncio = 2 am, CA = 2 AO, então o triângulo DAC é semelhante ao triângulo mao e, consequentemente, dc = 2 meses.

Um argumento semelhante permite afirmar que Cu é semelhante ao CON, onde Ca = 2 CO e CB = 2 CN. Segue -se que AB = 2 em.

Em suma, AB = 2 em y 2 meses. Então, quando saímos:

Ab + dc = 2 em + 2 meses = 2 (mo + on) = 2 mn

Finalmente limpa o MN:

Mn = (ab + dc) /2

E conclui -se que a mediana de um trapézio mede os corpos semi -Bases, ou em outras palavras: a mediana mede a soma das bases, dividida por dois.

Exemplo 3

Demonstrar que em um rombus as diagonais são cortadas em ângulos retos.

Figura 12. RHombus e demonstração de que suas diagonais são cortadas em ângulos retos. Fonte: f. Zapata.

O Conselho da Figura 12 mostra a construção necessária. Primeiro, o paralelogramo do ABCD é desenhado com ab = bc, que é um Rhombus. As diagonais CA e DB determinam oito ângulos mostrados na figura.

Usando o teorema (a.Yo.p.) que afirma que ângulos alternativos internos entre paralelos são cortados por um secante determinam ângulos iguais, podemos estabelecer o seguinte:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ e Δ2 = β2. (*)

Por outro lado, como os lados adjacentes de um rombus são de igual comprimento, quatro triângulos isósceles são determinados:

DAB, BCD, CDA e ABC

Agora, o teorema dos triângulos (isósceles) é invocado que afirma que os ângulos adjacentes à base são de igual medida, onde se conclui que:

δ₁ = β2, Δ2 = β₁, α2 = γ₁ e α₁ = γ2 (**)

Se os relacionamentos (*) e (**) forem combinados, a próxima igualdade de ângulos é alcançada:

α₁ = α2 = γ₁ = γ₁ Por um lado e β₁ = Β2 = δ₁ = Δ2 para o outro. 

Lembrando o teorema dos triângulos iguais que afirmam que dois triângulos com um lado igual entre dois ângulos iguais são os mesmos:

AOD = AOB e, consequentemente, também os ângulos ∡AOD = ∡AOB.

Então ∡AOD + ∡AOB = 180º, mas como ambos os ângulos são de igual medida, 2 ∡AOD = 180º, o que implica que ∡AOD = 90º.

Isto é, é demonstrado geometricamente que as diagonais de um rombus são cortadas em ângulos retos.

Exercícios resolvidos

- Exercício 1

Demonstre que em um trapézio retangular, ângulos não OG são suplementares.

Solução

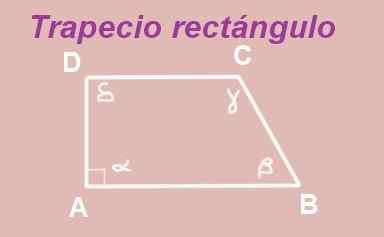Figura 13. Trapézio retângulo. Fonte: f. Zapata.

O trapézóide ABCD é construído com bases paralelas AB e DC. O ângulo interno do vértice A é reto (mede 90º), então você tem um trapézico retangular.

Os ângulos α e δ são ângulos internos entre dois paralelos paralelos AB e DC, portanto são os mesmos, ou seja, δ = α = 90º. 

Por outro lado, foi demonstrado que a soma dos ângulos internos de um quadrilateral adiciona 360º, ou seja::

α + β + γ + Δ = 90º + β + 90º + δ = 360º.

O acima leva a:

 β + δ = 180º

Confirmando o que queria demonstrar que os ângulos β e δ são suplementares.

- Exercício 2

Um paralelogramo ABCD tem AB = 2 cm e AD = 1 cm, além disso, o ângulo ruim é 30º. Determine a área do referido paralelogramo e o comprimento de suas duas diagonais.

Solução

A área de um paralelogramo é o produto do comprimento de sua base pela altura. Nesse caso, o comprimento do segmento b = ab = 2 cm será tomado como base, o outro lado tem comprimento a = ad = 1 cm e a altura h será calculada da seguinte forma:

H = ad * sin (30º) = 1 cm * (1/2) = ½ cm.

Então: área = b * h = 2 cm * ½ cm = 1 cm².

Referências

1. C. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
2. Campos, f., CERECEDO, f. J. (2014). Matemática 2. Grupo editorial da Patria.
3. Libertado, k. (2007). Descubra polígonos. Companhia de Educação de Benchmark.
4. Hendrik, v. (2013). Polígonos generalizados. Birkhäuser.
5. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.
6. Jr. Geometria. (2014). Polígonos. Lulu Press, Inc.
7. Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
8. Patiño, m. (2006). Matemática 5. Editorial Progreso.
9. Wikipedia. Quadriláteros. Recuperado de: é.Wikipedia.com