Proporcionalidade constante o que é, cálculo, exercícios

O proporcionalmente constante É um elemento numérico relacional, usado para definir o padrão de similaridade entre 2 magnitudes que são alteradas simultaneamente. É muito comum representá -lo como uma função linear genérica através da expressão f (x) = k.X. No entanto, essa não é a única representação de uma possível proporcionalidade.

Por exemplo, a relação entre x e y na função y = 3x tem uma constante de proporcionalidade igual a 3. Isso mostra que quando a variável independente x cresce, o mesmo acontece com a variável dependente e, no triplo de seu valor anterior.

As alterações aplicadas em uma variável têm repercussões imediatas, por outro, para que haja um valor conhecido como constante de proporcionalidade. Isso serve para relacionar as diferentes magnitudes que ambas as variáveis ​​adquirem.

[TOC]

Qual é a constante de proporcionalidade e tipos

De acordo com a tendência de mudar as variáveis, as proporcionalidades podem ser classificadas em 2 tipos.

Proporcionalidade direta

Sugere uma relação unidirecional entre duas magnitudes. Nele, se a variável independente apresentar algum crescimento, a variável dependente também crescerá. Da mesma forma, qualquer diminuição na variável independente causará uma diminuição na magnitude de e.

Por exemplo, a função linear usada na introdução; Y = 3x, corresponde a uma proporção direta de proporcionalidade. Isso ocorre porque o aumento da variável independente x causará um aumento no triplo no valor anterior obtido pela variável dependente e.

Da mesma forma, a variável dependente diminuirá seu valor quando x descer em magnitude.

O valor da constante de proporcionalidade "k" em um relacionamento direto é definido como k = y/x.

Proporcionalidade inversa ou indireta

Nesse tipo de funções, a relação entre as variáveis ​​é apresentada de maneira antônima, onde o crescimento ou diminuição da variável independente corresponde, respectivamente, à diminuição ou crescimento da variável dependente.

Pode servir a você: Decomposição de números naturais (exemplos e exercícios)

Por exemplo, a função f (x) = k/x é uma relação inversa ou indireta. Como o valor da variável independente começa a aumentar, o valor de k será dividido por uma figura crescente, tornando a variável dependente diminuição do valor de acordo com a proporção.

De acordo com o valor obtido por K, a tendência da função inversa proporcional pode ser definida. Se k> 0, então a função diminuirá em todos os números reais. E seu gráfico estará localizado no 1º e 3º quadrante.

Pelo contrário, se o valor de k for negativo ou menor que zero, a função estará aumentando e seu gráfico será encontrado no 2º e 4 quadrante.

Como é calculado?

Existem diferentes contextos em que a definição da constante de proporcionalidade pode ser necessária. Em diferentes casos, diferentes dados sobre o problema serão mostrados, onde o estudo destes finalmente mostrará o valor de k.

De maneira genérica, os mencionados podem ser recapitulados. Os valores de k correspondem a duas expressões de acordo com o tipo de proporcionalidade presente:

- Direto: k = y/x

- Inverso ou indireto: k = y.X

De acordo com o seu gráfico

Às vezes, apenas o gráfico de uma função será conhecido parcial ou completamente. Nesses casos, será necessário, por análise gráfica, determinar o tipo de proporcionalidade. Em seguida, teremos que definir uma coordenada que permita verificar os valores de x e y para aplicar à fórmula K correspondente.

Os gráficos referentes a proporcionalidades diretas são do tipo linear. Por outro lado, os gráficos de funções proporcionais inversas geralmente tomam forma de hiperbolas.

De acordo com a tabela de valores

Em alguns casos, há uma tabela de valores com os valores correspondentes a cada iteração da variável independente. Normalmente, isso implica a realização do gráfico, além de definir o valor de k.

Pode servir a você: distribuição de frequência: como fazer uma tabela, exemplo, exercício

De acordo com a expressão analítica

Mostra a expressão que define analiticamente. Diretamente o valor de k pode ser claro, ou também pode ser inferido da própria expressão.

Como regra de três diretos ou compostos

Em outros modelos de exercícios, existem certos dados, que se referem à relação entre valores. Isso torna necessário a aplicação de três diretos ou compostos para definir outros dados necessários no ano.

História

O conceito de proporcionalidade sempre esteve presente. Não apenas na mente e no trabalho dos grandes matemáticos, mas na vida cotidiana da população, devido à sua praticidade e aplicabilidade.

É muito comum atender a situações que exigem uma abordagem de proporcionalidade. Estes são apresentados em cada caso em que variáveis ​​e fenômenos são comparados que mantêm certos relacionamentos.

Através de uma linha do tempo, podemos caracterizar momentos históricos, nos quais os avanços matemáticos sobre a proporcionalidade foram aplicados.

- Segundo século a.c. O sistema de armazenamento de fração e proporções na Grécia é adotado.

- Século V a.c. A proporção que relaciona o lado e a diagonal de um quadrado também é descoberta na Grécia.

- 600 a.c. Tales de Mileto apresenta seu teorema em relação à proporcionalidade.

- Ano 900. O sistema decimal usado anteriormente pela Índia em razões e proporções é estendido. Contribuição feita pelos árabes.

- XVII Século. As contribuições se referem às proporções no cálculo da chegada de Euler.

- Século XIX. Gauss fornece o conceito de número e proporção complexos.

- Século XX. Proporcionalidade como modelo de função é definida por açúcar e deulofeo.

Exercícios resolvidos

Exercício 1

É necessário para calcular o valor das variáveis ​​x, y, z e g. Conhecendo os seguintes relacionamentos proporcionais:

3x + 2y - 6z + 8g = 1925

Pode atendê -lo: variável aleatória contínua

x/3 = y/8 = z/3 = g/5

Os valores relativos da constante de proporcionalidade são definidos. Estes podem ser obtidos a partir do segundo relacionamento, onde o valor que divide cada variável indica um relacionamento ou razão sobre k.

X = 3k y = 2k z = 3k g = 5k

Os valores são substituídos na primeira expressão, onde o novo sistema será avaliado em uma única variável K.

3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9k + 4k -18k + 40k = 1925

35K = 1925

K = 1925/35 = 55

Usando esse valor da constante de proporcionalidade, podemos encontrar a figura que define cada uma das variáveis.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Exercício 2

Calcule a constante de proporcionalidade e a expressão que define a função, dadas seus gráficos.

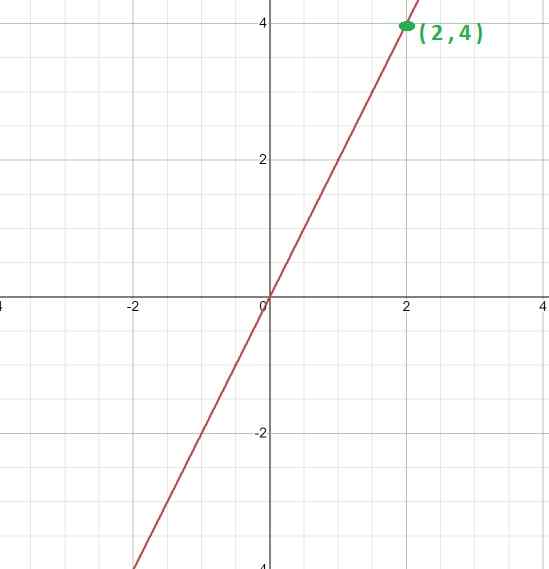
Primeiro, o gráfico é analisado, seu caráter linear sendo evidente. Isso indica que é uma função com proporcionalidade direta e que o valor de k será obtido através da expressão k = y/x

Então um ponto determinável do gráfico é escolhido, ou seja, um em que as coordenadas que o compõem podem ser exatas.

Para este caso, o ponto é levado (2, 4). Onde podemos estabelecer o seguinte relacionamento.

K = 4/2 = 2

Para que a expressão seja definida pela função y = kx, que para este caso será

F (x) = 2x

Referências

1. Matemática para eletricidade e eletrônica. Dr. Arthur Kramer. Cengage Learning, 27 de julho. 2012
2. Visão 2020: O papel estratégico da pesquisa operacional. N. Ravichandran. Editores aliados, 11 de setembro. 2005
3. Conhecimento gramatical e aritmético do assistente administrativo do estado.e-book. Mad-eduform
4. Reforço de Matemática para Suporte e Diversificação Curricular: Para Suporte Curricular e Diversificação. Mª Lourdes Lázaro Soto. NARCEA DICIONES, 29 de agosto. 2003
5. Logística e gerenciamento comercial. Maria José Escudero Serrano. Edições paraninfo, S.PARA., 1º de setembro. 2013