Circuito elétrico misto

Explicamos o que é um circuito misto, suas características, partes, símbolos e damos vários exemplos

O que é um circuito misto?

Ele Circuito elétrico misto É aquele que contém elementos conectados tanto em série quanto em paralelo, de modo que, ao fechar o circuito, diferentes tensões e correntes são estabelecidas em cada uma delas.

Os circuitos são projetados com uma ampla variedade de objetivos e seus elementos pertencem a duas categorias: ativos e passivos.

Os elementos ativos do circuito são geradores ou tensão ou fontes de corrente, diretas ou alternativas. Por outro lado, os elementos passivos são a resistência, os capacitores ou capacitores e as bobinas. Tanto um quanto outros admitem conexões em série e paralelos, bem como combinações destes.

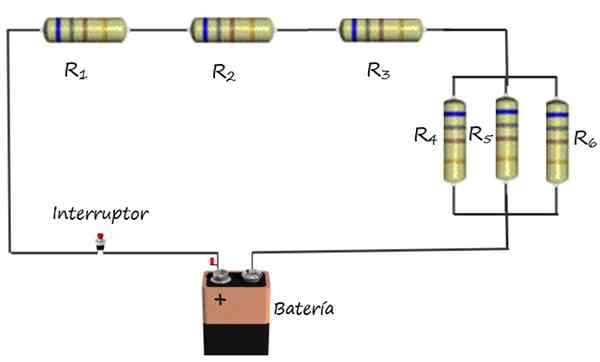
A figura superior mostra, como exemplo, uma associação mista de resistências elétricas com uma bateria e um interruptor. Resistências r₁, R₂ e r₃ Eles estão associados em série, enquanto resistores r₄, R₅ e r₆ Eles estão conectados em paralelo.

Outras conexões possíveis, diferentes das associações paralelas em série, são delta (ou triângulo) e estrela, freqüentemente usadas em máquinas elétricas alimentadas com corrente alternada.

Características de um circuito misto

Em geral, o seguinte é observado em um circuito misto:

• A alimentação do circuito pode ser através de um gerador direto (bateria) ou alternativo.
• Considera -se que os cabos ou fios que unem os diferentes elementos não oferecem resistência atual.
• Tanto a tensão quanto a corrente podem ser constantes ou variáveis ​​no tempo. Letras maiúsculas são usadas para denotar valores constantes e minúsculas quando variável.
• Em circuitos mistos puramente resistentes, a corrente através das resistências em série é a mesma, enquanto em resistências paralelas em geral é diferente. Para calcular a corrente e a tensão em cada resistência, o circuito é geralmente reduzido a uma resistência única, chamada resistência equivalente ou r_Eq .

Pode servir a você: subtração vetorial: método gráfico, exemplos, exercícios

Resistências em série

Resistências em paralelo

• Se o circuito consistir em n capacitores, quando a capacitância equivalente C está associada em série_Eq resultado:

Capacitores da série

Capacitores paralelos

• As bobinas ou indutores seguem as mesmas regras de associação que a resistência. Assim, quando você deseja reduzir uma associação de bobinas em série para obter a indutância equivalente l_Eq, As seguintes fórmulas são usadas:

Indutores em série

Indutores em paralelo

• Para resolver os circuitos mistos com resistores, a lei ohm e as leis de Kirchoff são usadas. Em circuitos resistentes simples, a lei de Ohm é suficiente, mas para redes mais complexas é necessário presente.

Relação entre tensão e corrente

Dependendo do elemento de circuito, há uma relação entre a tensão ou tensão através do elemento com a intensidade da corrente que passa por ele:

Resistência r

A lei de Ohm é usada:

v_R(t) = r ∙ i_R(T)

Capacitor c

Indutância l

Partes de um circuito misto

Em um circuito elétrico, as seguintes peças são distinguidas:

Nó

Ponto de união entre dois ou mais fios condutores que conectam alguns passivos ativos ou do circuito.

Filial

Elementos, ativos ou passivos, que estão entre dois nós consecutivos.

Malha

Parte fechada do circuito viajou sem passar duas vezes pelo mesmo ponto. Pode ou não ter um gerador de tensão ou atual.

Leis ou regras de Kirchoff

As regras de Kirchoff aplicam -se se as correntes e as tensões são constantes ou se dependem do tempo. Embora sejam geralmente chamados de leis, são regras para aplicar princípios de conservação a circuitos elétricos.

Pode atendê -lo: física de estado sólido: propriedades, estrutura, exemplos

Primeira regra

Estabelece o princípio de conservação da carga, apontando que a soma das intensidades atuais que entram em um nó, equivalente à soma das intensidades que surgem dela:

∑ i_Entrada = ∑ i_saída

Segunda regra

Nesta ocasião, o princípio da conservação de energia é estabelecido, quando afirma que a soma algébrica de tensões em uma parte fechada do circuito (malha) é zero.

∑ vi = 0

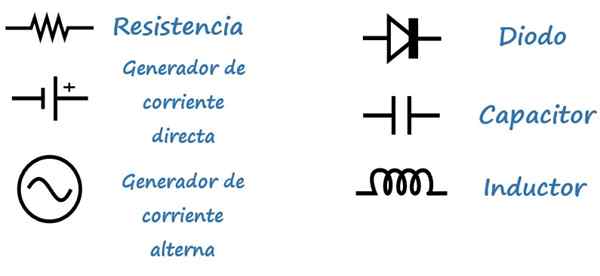
Símbolos

Para facilitar a análise dos circuitos, são usados ​​os seguintes símbolos:

Exemplos de circuito misto

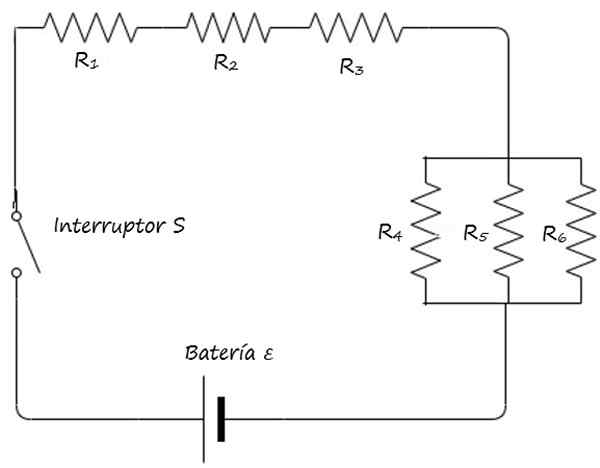
Exemplo 1

Desenhe o circuito misto da figura inicial compacta, usando os símbolos descritos acima.

Responder

Exemplo 2

No circuito do Exemplo 1, você tem os seguintes valores para resistores e bateria:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

Para o circuito mostrado, a bateria é considerada ideal, ou seja, não possui resistência interna. Normalmente, as baterias reais têm uma pequena resistência interna que é desenhada em série com a bateria e é tratada da mesma forma que as outras resistências no circuito.

Calcule o seguinte:

• a) a resistência equivalente do circuito.
• b) o valor da corrente que sai da bateria.
• c) as tensões e correntes em cada uma das resistências.

Responda para

O primeiro grupo de resistências: r₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω estão conectados em série, portanto, a resistência equivalente é r₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

Pode servir a você: Terceira Lei da Termodinâmica: Fórmulas, Equações, Exemplos

Quanto ao grupo de resistência R₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω, são conectados em paralelo e a fórmula correspondente deve ser aplicada:

 O resultado recíproco ou inverso do resultado anterior é a resistência equivalente ao grupo:

R₄₅₆ = 12 Ω

O circuito simplificado obtido é mostrado no gráfico a seguir, consistindo em duas resistências em série com a bateria ou a bateria. Essas duas resistências são adicionadas para encontrar a resistência equivalente do circuito R original_Eq:

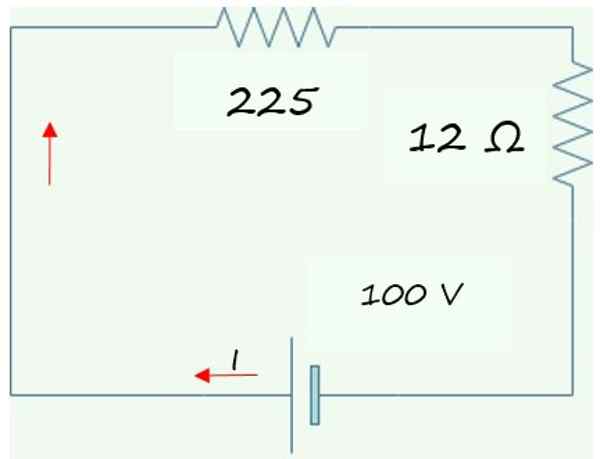
R_Eq= 225 Ω + 12 Ω = 237 Ω

Resposta b

A corrente que deixa a bateria (por convenção é sempre desenhada pelo pólo positivo) é calculado com o circuito simplificado, que consiste na resistência equivalente r_Eq em série com a bateria, à qual a lei de Ohm é aplicada:

ε = i · r

I = ε / r = 100 v / 237 Ω = 0.422 a

Resposta c

Tensões e correntes em cada uma das resistências da SA calculam pela lei de Ohm. A primeira coisa que é observada é que a corrente que sai da bateria atravessa totalmente as resistências r₁ , R₂ e r₃ E, em vez disso, é dividido cruzando r₄ , R₅ e r₆.

As tensões v₁, V₂ e V₃ são:

V₁  = 0.422 a × 50 Ω = 21.1 v
V₂  = 0.422 a × 100 Ω = 42.2 v
V₃  = 0.422 a × 75 Ω = 31.7 v

Por sua parte, Voltajes V₄, V₅ e V₆ Eles têm o mesmo valor, já que as resistências estão em paralelo:

V₄ = V₅ = V₆ = 0.422 a × 12 Ω = 5.06 v

E as respectivas correntes são:

Yo₄ = 5.06 V / 24 Ω = 0.211 a

Yo₅ = I₆ = 5.06 v / 48 Ω = 0.105 a

Observe que adicionando eu₄, Yo₅ e eu₆ A corrente total que sai da bateria é obtida novamente.