Propriedades do centro de gravidade, cálculo, exemplos

Ele Centro de gravidade de um corpo de tamanho mensurável é o ponto em que seu peso é considerado aplicado. É, portanto, um dos principais conceitos de estática.

A primeira abordagem nos problemas da física elementar é assumir que qualquer objeto se comporta como uma massa específica, ou seja, falta dimensões e toda a massa está concentrada em um único ponto. Isso é válido para uma caixa, um carro, um planeta ou uma partícula subatômica. Este modelo é conhecido como Modelo de partículas.

figura 1. Na altura, salta, o atleta os conserta para que seu centro de gravidade esteja fora do corpo. Fonte: Pixabay

Naturalmente, essa é uma abordagem, que fornece resultados muito bons para muitos aplicativos. Não é uma tarefa fácil considerar o comportamento individual dos milhares e milhões de partículas que qualquer objeto pode conter.

No entanto, as dimensões reais das coisas devem ser levadas em consideração se você quiser. Como geralmente estamos nas imediações da terra, a força sempre presente em qualquer corpo é precisamente o peso.

[TOC]

Considerações para encontrar o centro de gravidade 

Se o tamanho do corpo for levado em consideração, onde o peso será aplicado especificamente? Quando você tem um objeto contínuo arbitrariamente, seu peso é um Força distribuída entre cada uma de suas partículas constituintes.

Deixe essas partículas m₁, m₂, m₃… Cada um deles experimenta sua força gravitacional correspondente m₁g, m₂g, m₃G ..., tudo paralelo. É assim, uma vez que o campo gravitacional da Terra é considerado constante na grande maioria dos casos, tendo em vista o fato de que os objetos são pequenos em comparação com o tamanho do planeta e estão próximos de sua superfície.

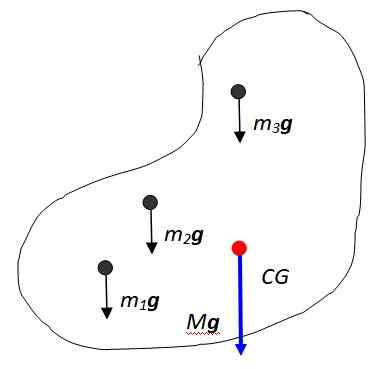Figura 2. O peso do objeto é uma massa distribuída. Fonte: Self feito.

A soma vetorial dessas forças resulta no peso do objeto, aplicado ao ponto chamado centro de gravidade denotado na figura como CG, que então coincide com o Centro de massa. O centro de massa, por sua vez, é o ponto em que toda a massa pode ser considerada concentrada.

O peso resultante tem magnitude Mg onde M É a massa total do objeto e, é claro, é direcionado verticalmente para o centro da terra. A notação de Sumory é útil para expressar o corpo total do corpo:

Objetos simétricos e homogêneos, que são equivalentes à sua densidade sendo uniformes, têm seu centro de gravidade no centro geométrico: cubos, paralelepípedes, anéis, pneus ou esferas.

O centro de gravidade nem sempre corresponde a um ponto de material. Por exemplo, o CG de um aro está em seu centro geométrico, onde não há nenhuma massa. Mesmo assim, se você deseja analisar as forças que agem em um aro, o peso deve ser aplicado a este ponto preciso.

Em que casos em que o objeto é arbitrário, se for homogêneo, seu centro de massa ainda pode ser calculado ao encontrar o centróide Ó baricentro da figura.

Pode atendê -lo: Mercúrio (planeta)

Como o centro de gravidade é calculado?

Em princípio, se o centro de gravidade (CG) e o centro de massa (CM) coincidem quando o campo gravitacional é uniforme, o CM pode ser calculado e, nele, aplicar o peso.

Considere dois casos: o primeiro é aquele em que a distribuição de massa é discreta; isto é, você pode contar cada massa que forma o sistema e atribuir um número I, como foi feito no exemplo anterior.

As coordenadas do centro de massa para uma distribuição de massa discreta são: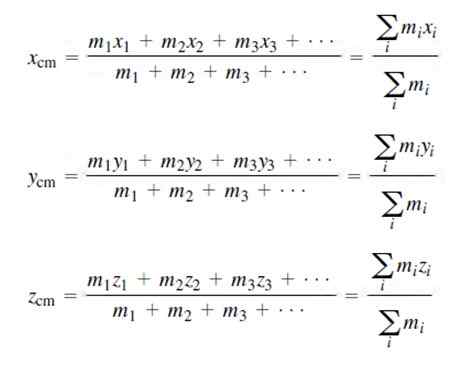

Naturalmente, a soma de todas as massas é equivalente à massa total do sistema M, como indicado acima.

As três equações são reduzidas a uma forma compacta ao considerar o vetor r_cm o Vetor de posição do centro de massa:

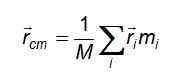
E, em caso de distribuição contínua de massa, onde as partículas são de tamanho diferencial e não podem ser distinguidas para contá -las, a soma é substituída por uma parte integrante feita sobre o volume ocupado pelo objeto em questão:

Onde r É o vetor de posição de uma massa diferencial Dm E a definição de densidade de massa para expressar o diferencial de massa foi feita Dm contido em um diferencial de volume Dv:

A densidade do objeto pode ser constante; nesse caso, sai da integral, ou sendo uma função das coordenadas espaciais e devemos conhecer sua dependência (x, y, z) para resolver a integral.

Propriedades

Algumas considerações importantes sobre o centro de massa são as seguintes:

- Embora seja necessário um sistema de referência para estabelecer posições, o centro de massa não depende da escolha feita do sistema, pois é uma propriedade do objeto.

- Quando o objeto tem um eixo ou um plano de simetria, o centro de massa está no referido eixo ou plano. Aproveite essa circunstância economiza tempo de cálculo.

- Todas as forças externas que atuam no objeto podem ser aplicadas ao centro de massa. Seguir a faixa deste ponto, dá uma idéia global do movimento do objeto e facilita o trabalho de estudar seu comportamento.

-Encontrando o centro de gravidade de um corpo em equilíbrio estático

Suponha que o corpo da figura anterior esteja em equilíbrio estático seja.

Figura 3. Esquema para calcular o torque do peso em relação ao ponto ou.

O momento da torção líquida em relação a O, de acordo com a Figura 3 é: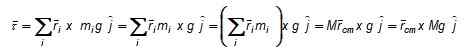Uma força f aplicada verticalmente no centro da gravidade (ou também acima ou abaixo, no eixo que passa por ele) produziria uma torção oposta que impediria a rotação do objeto e manteria o equilíbrio rotacional. A magnitude de F é escolhida para que o objeto também não seja transferido e, dessa forma, teremos em equilíbrio estático.

Pode atendê -lo: Óptica ondulada

-Exemplo resolvido

Uma barra fina de material uniforme tem um comprimento de 6 me pesa 30 N. No final, um 50 N oeste e outro de 20 N na extremidade direita são enforcados. Encontre: a) a magnitude da força ascendente necessária para manter o equilíbrio da barra, b) o centro de gravidade do conjunto.

Solução

O diagrama das forças é mostrado na figura a seguir. O peso da barra é aplicado em seu centro de gravidade, que coincide com seu centro geométrico. A única dimensão da barra levada em consideração é o seu comprimento, já que a declaração informa que é fina.

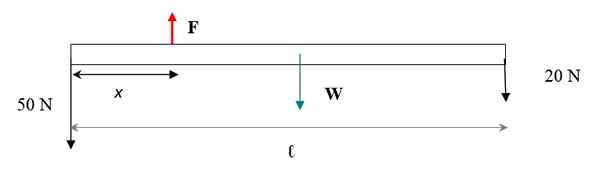Figura 4. Diagrama de Pàra La Barra.

Para que o sistema de peso bar + permaneça em equilíbrio de tradução, a soma das forças deve ser nula. As forças são verticais, se considerarmos uma placa + e abaixo com um sinal - então:

F- 50- 20-30 n = 0

F = 100 n

Esta força garante o equilíbrio da tradução. Tomando os momentos de torção de todas as forças em relação a um eixo que passa pela extremidade esquerda do sistema e aplicando a definição:

t = r x f

Os momentos de todas essas forças em relação ao ponto selecionado são perpendiculares ao plano da barra:

t_F = xf = 100x

t_C = -(l/2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Desde a força de 50 N passa pelo eixo de volta selecionado e não exerce momento)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Portanto:

100 x -90 -120 n.M = 0

x = 2.10 m

O centro de gravidade da barra bar + pesos está localizado em 2.10 metros da extremidade esquerda do bar.

Diferença com o centro de massa

O centro de gravidade coincide com o centro de massa, como indicado, desde que o campo gravitacional da terra seja constante para todos os pontos do objeto a serem considerados. O campo gravitacional da terra não é nada além do valor bem conhecido e familiar de g = 9.8 m/s² direcionado verticalmente para baixo.

Embora o valor de g experimente variações com latitude e altitude, elas geralmente não afetam objetos sobre os quais a maioria das vezes é tratada. Muito diferente seria se for considerado um corpo grande nas proximidades da terra, por exemplo, um asteróide que se aproximaria do planeta.

O asteróide tem seu próprio centro de massa, mas seu centro de gravidade não precisaria mais coincidir com isso, já que g Provavelmente experimentaria variações substanciais de magnitude, dado o tamanho do asteróide e que os pesos de cada partícula podem não ser paralelos.

Outra diferença fundamental é que o centro de massa é independentemente de haver ou não uma força chamada peso aplicado no objeto. É uma propriedade intrínseca do objeto que revela como sua massa é distribuída em relação à sua geometria.

Pode atendê -lo: qual é a constante dielétrica?

O centro de massa existe ambos se houver peso aplicado como se não. E está localizado na mesma posição, embora o objeto seja transferido para outro planeta em que o campo gravitacional é diferente.

Por outro lado, o centro de gravidade está claramente ligado à aplicação de peso, pois fomos capazes de apreciar ao longo dos parágrafos anteriores.

Centro de Exemplos de Gravidade

Centro de gravidade de objetos irregulares

É muito fácil descobrir onde o centro de gravidade de um objeto irregular é como um copo. Primeiro, ele é suspenso de qualquer ponto e a partir daí é desenhado uma linha vertical (na Figura 5, é a linha Fuchsia na imagem esquerda).

Em seguida, é suspenso de outro ponto e uma nova vertical (linha turquesa na imagem certa) é desenhada. A interseção de ambas as linhas é o centro de gravidade do copo.

Figura 5 . CG Localização de um copo. Fonte: Pixabay modificado.

Equilíbrio de objetos

Vamos analisar a estabilidade de um caminhão que circula ao longo da estrada. Quando o centro de gravidade estiver acima da base do caminhão, ele não derramará. A imagem à esquerda é a posição mais estável.

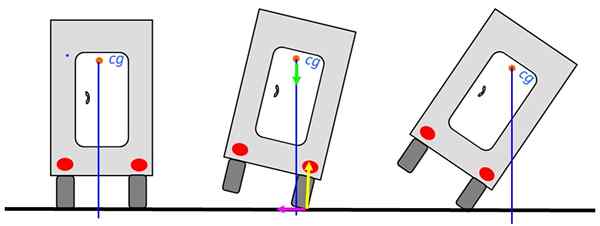Figura 6. Balance de caminhão. Fonte: Self feito.

Mesmo quando o caminhão se inclina para a direita pode retornar à posição estável de equilíbrio, como no desenho do meio, porque a vertical ainda passa pela base. No entanto, quando essa linha passa para fora do caminhão virará.

O diagrama mostra as forças no ponto de apoio: o normal em amarelo, o peso em verde e o atrito estático à esquerda em Fuchsia. Normal e lixo. Portanto, eles não contribuirão para despejar o caminhão.

O peso permanece, que exerce um momento de torção, felizmente no sentido anti -hemearário e que tende a retornar ao caminhão à sua posição de equilíbrio. Observe que a linha vertical passa pela superfície de suporte, que é o pneu.

Quando o caminhão está na posição da extrema direita, o tempo de torção das mudanças de peso e se torna em uma direção tensa. Não sendo capaz de ser neutralizado em outro momento, o caminhão derramará.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.  247-253.
2. Giancoli, d.  2006. Física: Princípios com aplicações. 6º ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V. 331-341.
4. Rex, a. 2011. Fundamentos da Física. Pearson.146-155.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.340-346.